
It is the month of Ramzan, and I am about to break the fast. The iftar hosted by the Muslim Students Association of Carleton University here in Ottawa, Canada, is a simple offering of dates and a samosa followed by dinner. The dates are three in number, following the 1445-year-old tradition of Muhammad ﷺ

With the number of dates complementing the edible triangle, I recalled my thirty-year-old Number 3 poem, devoted to that form whose very name, tri-angle, suggests the number.
No. 3
In chaos
The first enclosure
Angels have fled leaving
A kind of order inside
System trisecting the universe
With within without
Science
Is now possible
In a tent with pegs
Refixed further away
Each paradigm shifts
To increasing howling outside
The poem braided Thomas Kuhn (paradigm shifts), Karl Popper (a new theory does not overthrow but subsumes the previous one) and Jacob Bronowski (the scientific bird’s eye view keeps enlarging to reach the unattainable God’s eye-view). Number 3 was one of nine poems in my long poem Anatomy of Numbers: a series from one to nine with as many quatrains as the number it addressed. As the final minutes of the fast ticked away, rather than recall those forty-five quatrains (factorial nine), I recalled instead the Samosa riddle by the 13th-century polymath Amir Khusro, the Sufi poet, musician and scholar who is buried next to his guru Shaykh Khwaja Nizamuddin Auliya in Delhi. The 800-year-old riddle pairs two unlike statements that point to their resolution: Why wasn’t the samosa eaten and the shoe worn? The answer, lost in translation, is based on the rebus of the pun “talla” – meaning both “to fry” and “sole of footwear.”

Amir Khusro, while pioneering the Samosa genre in India, is late in the game. 8th-century polymath Ishaq al-Mawsili in Bagdad of the Abbasid Empire reputedly devoted a poem to “sambusak,” as it was initially called. Five hundred years later, the traveller-friendly snack would reach India via the trade route of Muslim Civilizations. 13th-century Amir Khusro and 14th-century traveller Ibn Battuta, who was in the court of Muhammad bin Tuqhluq, would continue to celebrate its meat filling. The 15th-century ruler of Malwa Sultanate Book of Delicacies (Ni’matnāmah Naṣir al-Dīn Shāhī) shows him being offered “sanbusa” that is inscribed informally above his head. Mandu would subsequently fall to the Mughals, who had their recipe of Samosas that they called qutab, which “the people of Hindustan call sanbúsah”. Following the recipe detailed in the 16th-century Mughal chronicle, The Ain-i-Akbari, you would find Akbar’s preference unbearably salty for your modern palate. To reach this plate, the crisp triangle with a soft core had journeyed a millennium and a half across the world and a history almost as old as Islam.

The samosa, like the triangle, is named after its form. The etymological dictionary Nişanyan Sözlük states that “It is derived from the Persian and Middle Persian word sih سه or sē سی “three,” i.e. triangle (itself from Latin triangulum meaning “three-cornered”). And that is where we probe the samosa’s triangular relationship to the primary Platonic solid: tetrahedron. It is in the manner of their respective making as the net along which a straight strip of paper folds into a tetrahedron, dough folds into a samosa, that bears kinship involving four triangles:

The lasting love triangle in India has fillings ranging from peas for Jains who shun root vegetables to the Bohri Keema Samosa for those who relish meat fillings like my friend Architect Keki. The other equivalent carnivore architect that comes to mind is R. Buckminster Fuller (or Bucky), who reasoned that with Earth’s 200 million square miles of spherical surface constantly exposed to the sun with its “syntropic, biochemical capability to photosynthetically convert stellar radiation falling on Earth into hydrocarbon vegetation that is in turn converted as “food” into all manner of biological proliferatings…” That is Bucky’s way of saying plants ate sunlight, animals ate plants, so eating animals offered the maximum sunshine bang for the buck. So when Keki and the pioneering Conservation Architect Kirti visited Canada, I took them past Moshe Safdie’s Habitat to see Bucky’s geodesic dome, a hangover of the seminal Expo-67 in Montreal.

Bucky had his samosa riddle:
How many triangles do you get if you add one triangle + one triangle?
Answer: Four triangles
1+1=4
If you answered, “2 triangles”, Bucky would disarm you with his smile (with the upper central incisor charmingly missing), saying, as in Synergetics 108:
Two triangles can and frequently do associate with one another, and in so doing they afford us with a synergetic demonstration of two prime events cooperating in Universe. Triangles cannot be structured in planes. They are always positive or negative helixes. You may say that we had no right to break the triangles open in order to add them together, but the triangles were in fact never closed because no line can ever come completely back into itself. Experiment shows that two lines cannot be constructed through the same point at the same time. One line will be superimposed on the other. Therefore, the triangle is a spiral a very flat spiral, but open at the recycling point.
Or, as another quatrain from Anatomy of Numbers (this time in Poem No.8) states:
Crossing lines either
Subway or flyover
Or one interrupts
To let the other pass
Seeing your eyes glaze over, Bucky’s smile would disappear, and his soft grey eyes would fix on you through his thick glasses fixed to his geodesic head with a rubber band. With utmost concentration and rapid-fire clipped speech, he would semi-bark to elaborate:
By conventional arithmetic, one triangle plus one triangle equals two triangles. But in association as left helix and right helix, they form a six-edged tetrahedron of four triangular faces. This illustrates an interference of two events impinging at both ends of their actions to give us something very fundamental: a tetrahedron, a system, a division of the Universe into inside and outside. We get the two other triangles from the rest of the Universe because we are not out of this world. This is the complementation of the Universe that shows up repeatedly in the way structures are made and in the way crystals grow. As separate actions, the two actions and resultants were very unstable, but when associated as positive and negative helixes, they complement one another as a stable structure.
In other words, if the triangle is a potential tetrahedron, then a samosa is a crypto tetrahedron. This is how he would resolve the riddle:
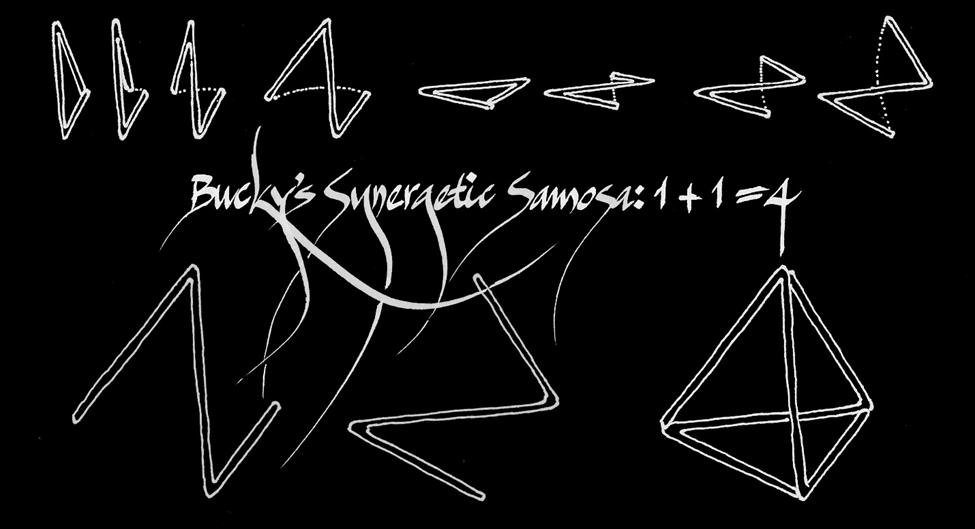
The tetrahedron was crucial to Bucky. The 60-degree coordination of the unfolding tetrahedron was the geometrical configuration that linked the physical world to the metaphysical, which he termed IVM or Isotropic Vector Matrix. Thinking mediated the two worlds, and thinking for Bucky had a geometric shape. Hence the subtitle of his magnum opus, the 1467 pages Synergetics: Explorations into the Geometry of Thinking in two wrist-bursting volumes. In my student years in architecture, it served as a parallel curriculum. Little wonder, in my beginning year, Milk Booth design, my proposal included reviving tetra packs invented in the 1940s that are easier to handle and pour and require less material to produce. They were made by sealing the milkbag at right angles for a stable tetrahedron. To open them, you snipped any one of the four corners.

In my intermediate year, the tetrapack’s 90-degree turn morphed into the staircase’s tread, a tetrahedron made of a pair of steel mesh hyperbolic paraboloids supporting a triangular glass tread. The stairway was in synch with the tetrahedral structure I had designed for a Tetra Hotel.
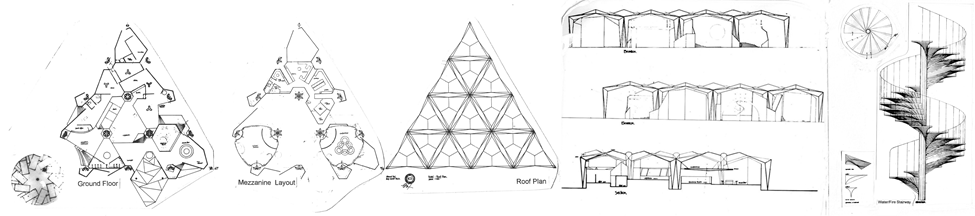
Imagine my delight in seeing the Hall of Nations, which was ten years old, when I visited Delhi as a freshly minted architect from Bombay during the IX Asian Games. Spaceframes worldwide were made of steel joints in the 1980s. But while India lacked steel, it didn’t lack ingenuity. The Hall of Nations was the acme of Desi Jugaad (you can’t get more nationalistic than that); India’s largest uninterrupted exhibition space was improvised using hand-poured concrete cast on site. Or, as Buckminster Fuller reportedly praised, “space-age building made with bullock cart technology,” The icon of structural expressionism put India on the modernist map: Raj karenge Raj Rewal aur Mahendra Raj.

The Asian Games motto was Fraternity Friendship Forever. Alas, such sporting spirit was nowhere in evidence thirty-five years later when the Hall of Nations succumbed to the mean-spirited philistines of Bulldozer Raj that bulldozed the Raj & Raj icon, leaving the alphabetical soup of impotent heritage bureaucrats of INTACH, ASI, and HCC wringing their hands. While a historical icon cannot shackle us from upgrading our infrastructure, neither should history be left shackled with a wannabe icon.
While the tetrahedron was virtually Bucky’s patent approach to solving structure, his protégé Ann Tyng became Louis Kahn’s lover, resulting in the uncharacteristic-of-Lou unbuilt-City-Tower. Bucky was the epitome of lightweight structures, and Lou was all gravitas. It was in the tetrahedral three-dimensional lattice of his Yale Gallery ceiling cast in concrete that Lou made the tetrahedron his own. He was the connoisseur of compression, while Bucky was the tension virtuoso. They were as unlike in their approaches as the crisp exterior of the samosa was to its soft filling. And yet it was in the cognitive dissonance of the two, like the counterpoint in music, that resulted in Bucky speaking at Lou’s funeral.

Louis Kahn would visit India at the invitation of Architect Doshi, who would also invite Bucky to Ahmedabad. I am sure Doshi would have served Bucky Samosas, albeit Veggies, where the pastry is thinner and crispier rather than thick and flakey, and it is more of a flattened cone in its folding than a pressed tetrahedron. Bucky’s itinerary was astutely choreographed by Doshi to transit via Bombay without stopping there, perhaps because Bombay was the domain of Charles Correa, the true inheritor of Bucky’s inventive approach, having studied under him both as an undergraduate at the University of Michigan and as a graduate student at MIT. Before Ahmedabad, Bucky was lecturing in New Delhi, where, in 1958, he delivered three talks on a single day. At each talk, he noticed a young woman in the first row. So, he presented her with a tensegrity sphere model, and she invited him home to meet her father, Nehru. Their meeting lasted over an hour, filled with Bucky’s rapid-fire monologue and the prime minister’s silence. That was the beginning of a lifelong friendship. Eleven years later, Indira Gandhi invited Bucky to deliver the Nehru Memorial Lecture in her inaugural year as Prime Minister.

In his “Ten Proposals for Improving the World,” Bucky puts an Indian spin on his ‘design science revolution’ :
The intellect, vision and courage of Mahatma Gandhi conceived of passive resistance with which bloodless revolution he broke the hold on India of history’s most powerful sovereignty. [But … ] passive resistance will not amplify the production of life support. In extension of the Mahatma’s magnificent vision, we are committed to the design science revolution by which it is possible bloodlessly to raise the standard of living of all humanity to a higher level of physical and metaphysical satisfaction than hitherto experienced or dreamed of by any humans.
This was vintage Bucky. It may have won over Indira Gandhi (his bio lists him as “Chief Architect, Completion of the Design for the International Airports at New Delhi, Bombay, and Madras” in 1973) but would not have convinced the Mahatama. But Gandhi would have yielded to his conjunction of “physical and metaphysical.” Just as in the Samosa, the crispness of the shell and the softness of contents coexist, so do Synergetics’s physical and metaphysical interface. It was why, when shown the Sri Yantra, Bucky exclaimed, “That’s an isotropic vector matrix,” (IVM) that lay at the heart of Synergetics as “an array of equilateral triangles which is seen as the comprehensive coordination frame of reference of nature’s most economical, most comfortable structural interrelationships employing 60-degree association and disassociation.” (Synergetics 420.02). Like his great aunt Margaret Fuller, Bucky was a transcendentalist, and the IVM was nature’s coordinate system for him.

At the centre of Sri Yantra was the bindu unmanifest, giving rise to the first move of the manifest: the innermost enclosing triangle. It is the original love triangle of Rishi, Devata, and Chanda, or the observer (1) observing (2) the observed (3). The succeeding layers of Sri Yantra encompass the manifestation of the universe.
This is the role of symbols: to connect the microcosm to the macrocosm, the inner reality within each of us, to the outer reality that surrounds all of us. Or, as Bucky used to say, “Unity is plural and at minimum two.” i.e. the samosa is both the crispness of the shell and the yielding of the centre; without the metaphysical centre, the physical is hollow, and without the physical, the metaphysical is unmoored. The ancient Sri Yantra and Bucky’s IVM unfold in tandem from the meditative centre to the far reaches of a cosmos whose centre is everywhere and circumference nowhere in sight.
“Intuition – A Metaphysical Mosaic”
by R. Buckminster Fuller.
Life’s original event
and the game of life’s
order of play
are involuntarily initiated
and inherently subject to modification
by the a priori mystery
within which consciousness first formulates
and from which enveloping and permeating mystery
consciousness never completely separates,
but which it often ignores
then forgets altogether
or deliberately disdains.
The connection between consciousness and cosmos, between earth and sky, is embodied in rituals like fasting during Ramzan. The azaan is an aural manifestation of that yearning, as is the form of the minaret, the physical quest to express the inexpressible metaphysical, as Hassan Fathy pointed out. We were standing on the terrace of his house and looking at the dark silhouette of the Sultan Hasan Madarssa Minaret – the tallest in medieval Cairo. “See how the minaret accelerates your vision upwards. It is divided into sections that rhythmically shorten the higher you go, like an accelerando in music. And the sections keep getting narrower, and their shapes change — from square to octagonal to cylindrical, adding to the acceleration.” Furthermore, classical minarets with three balconies express a spiritual ascent via stations of Islam (submission), Iman (faith), and Ihsan (righteousness), with the plan changing from the square of the earth via the intermediate octagon to the circle of heavens, even as the openings increase as you ascend in the growing light.
The azaan worldwide is based on the Middle Eastern maqam melodic system, which creates a mood that varies with the time of day. At Maghrib sunset, it is the maqam Segah, with its short duration comprised of its scales’ rise and fall. While the samosa tempts us, we reach first for a date to commemorate the tradition of Muhammad ﷺ breaking fast with three dates.
Even before the azaan ends, we are feasting on samosas. As Dunyahaigol suggests, Sath khane se samosa, badh jaatha hai bharosa: Eating Samosas together increases trust in each other.

Author’s Note: Anatomy of Numbers was first recited at the artist Anjana Mehra’s “Urban Seasons” Vernissage in 1995 at the National Centre for the Performing Arts in Mumbai and recently published as a calligraphic long poem in Sikandarah: Calligraphy, Epigraphy, Geometry, Islimi, Poetry, Photography (Y D Pitkar, Richa Raut & H Masud Taj. New Delhi: Copal Publishing 2024). An account of Bucky’s meeting with Indra Gandhi and Nehru is given by Alden Hatch in Buckminster Fuller -At Horne in the Universe (NY: Crown 1974, pp. 214-15); Bucky’s free verse Intuition: a Metaphysical Mosaic is in Ekistics 30:179 p. 256-260. “Ten Proposals for Improving the World,” is the final chapter of Earth Inc 1973 p.173-180. Scott Eastham showed Bucky the Sri Yantra and elicited his correlation with the IVM in American Dreamer (2007). The PDF of several illustrations and calligrams in this essay can be freely downloaded from the author’s Academia: Calligraphy.



